10.10.2010

Material ten zostal zaczerpniety ze stron internetowych ogolnodostepnych i nie byl chroniony prawami autorskimi gdyby jednak autorzy mieli jakiekolwiek pretensje to prosze o kontakt , proboje zebrac jak najwieksza ilosc dobrego, zetelnego materialu i scalic to w jednosc na mojej witrynce, napewno poprosilbym o prawo publikacji , aby mlodzi adepci modelarstwa mieli to wszystko w jednolitej calosci nie szukajac godzinami temataow w internecie , cel jest jeden zetelna informacja ogolnodostepna,
nie jest to proba podszywania sie pod autorow i podpisywaniem sie pod tym , gdybym znal poniektorych autorow napewno podpisalbym to w ich imieniu ....
Prawdziwe modelarstwo lotnicze to przyjemnie spedzone chwile na lotnisku w milej atmosferze, poprzedzone oczywiscie mniej lub bardziej czasochlonnym przygotowaniem modelu do lotu.
Minimum aby w ogóle myslec o lataniu.
1)
odkupic gotowy do lotu model -
wystarczy pomoc zaawansowanego modelarza,
zabudowa aparatury sterujacej i w góre ...
plusy:
nie tracimy czasu na budowe modelu, uczymy sie szybko latac….
minusy:
dalej stoimy w miejscu z majsterkowaniem i nie poznamy jego konstrukcji
2)
kupic model prawie gotowy do lotu "ARF"-
podobnie jak w punkcie 1)
3)
kupic gotowy model do pokrycia "ARC"-
podobnie jak w punkcie 1)
z tym, ze musimy poswiecic troche czasu (kilka dni) i troche grosza, i
rolke SOLAFILMU na oklejenie modelu
4)
kupic zestaw do samodzielnego montazu "KIT" -
w tym punkcie modelarz powinien posiadac „troche”zdolnosci manualnych. Po konsultacji z bardziej zaawansowanym kolega lub instruktorem w Modelarni powinien dac sobie rade.
tyczy sie poczatkujacych modelarzy chcacych budowaæ modele
5)
zbudowaæ model wedlug gotowego planu-
modelarz powinien znac podstawowe konstrukcje, umiec czytac plany modelarskie i miec juz na swoim koncie kilka modeli wykonanych z zestawu.
--juz dosc pracochlonny wariant.
6) zaprojektowaæ model i wykonac go w calosci samodzielnie -
nalezy zapoznac sie z podstawami konstruowania modeli latajacych kierowanych radiem oraz poznac podstawowe konstrukcje modelarskie.
- najbardziej pracochlonny wariant.
W kazdym z powyzszych wariantów niezbedne jest zabudowanie aparatury
sterujacej, w skrucie RC (radio control )
Jest rzecza oczywista, ze po pierwszym wyborze dokonamy nastepnego. Tak wiec, po zbudowaniu kilku modeli z zestawu pewnie bêdziemy chcieli wykonac model na podstawie skopiowanych od kolegi lub sciagniêtych z Internetu planów - to normalne.
Ja osobiscie polecam rozpoczac od punktu 4-tego i to od kupna zestawu od podstaw modelu szybowca swobodnie latajacego.
Dlaczego ???
Po pierwsze, nauczymy sie czytac rysunek techniczny, po drugie poznamy podstawy obróbki róznych materialów jak, drewna, balsy, depromu, sposobów ich oklejenia, pokrywania , malowania i przyblizymy sobie wiedzê na temat teorii budowy modeli i z czasem ich ulepszania i poprawiania bledów konstrukcyjnych .
Nie wspomne o takich drobnych sprawach ksztaltujacych Charakter…jak
dokkladnosc, cierpliwosc , podejmowania odpowiednich przemyslanych decyzji,
przydaje sie takze nabyta w szkole wiedza na temat fizyki, mechaniki , matematyki i materialoznastwo itp.
W ten sposób rozpoczyna sie prawdziwa niekoñczaca sie przygoda z modelarstwem lotniczym.
Jesli chcialbys budowac radiomodele samolotów,
musisz zdawaæ sobie sprawe, ze jestec zalezny od kilku czynników, które zadecyduja o losach Twojego hobby. Czynniki te postaralem sie zebrac w zbiór kilku pytañ na które powinienec sobie odpowiedziec, a mianowicie:
- Na jakim mieszkam terenie ? plaski, pagórkowaty, górzysty
- Czy w mojej okolicy znajduje sie aeroklub, nieczynne lotnisko, laka z koszona trawa, z dzika trawa ?
- Do czego ma sluzyc model ?
Ogólnie rzecz biorac w gre wchodzi: model szybowca do lotów termicznych, do lotów na zboczu, model samolotu akrobacyjnego czy tez makieta prawdziwego samolotu ? - Jaki chcialbym miec naped: silnik spalinowy czy elektryczny ?
- Jaka kwote pieniedzy chce przeznaczyc na poczatek ?
- Gdzie mogê sie zaopatrywac w artykuly modelarskie ?
- Czy mam dostêp do jakiegos warsztatu : stabilny stól, imadlo troche narzedzi itp. ?
To, na jakim terenie mieszkasz, moze miec duzy wplyw na wybór modelu jaki mozesz wybrac. Dokladniej mówiac, jesli w poblizu Twojego domu znajduje siê aeroklub, wiêc teoretycznie masz mozliwosc startowac i ladowaæ duzym modelem z silnikiem spalinowym. Piszê "teoretycznie", poniewaz najpierw powinienes zapytac kompetentna osobe, czy takie loty sa dopuszczalne. Zwykle bywa tak, ze nalezy byc czlonkiem owego aeroklubu, aby móc korzystac z pasa startowego. Jezli nie ma w Twoim sasiedztwie lotniska sportowego wtedy zmuszony jestes poszukac odpowiednio duzej laki. Wielkosc laki bedzie miala duzy wplyw na wielkosc modelu i rodzaj zastosowanego napedu. Jezli mieszkasz w terenie górzystym, masz szanse wystartowac szybowcem bez dodatkowego napedu, wykorzystujac duza prêdkosc wiatru na zboczu góry a pózniej latac w termice. Aby móc odpowiedziec na powyzsze pytania powinienes na poczatek przegladac strony internetowe z ta tematyka i fora dyskusyjne tam znajdziesz wiele odpowiedzi na nurtujace cie pytania.
A teraz kilka uwag na temat zakupow odpowiednich modeli urzadzeñ i wyposazenia:
1. Rób przemyslane zakupy - czasem warto dolozyc troche grosza aby zaoszczedzic sobie niepotrzebnego klopotu np. nadajnik, odbiornik, serwa przynyjmniej 6 kanalow
2. Nie porywaj sie z motyka na sloñce - pomimo, ze dysponujesz duzym pasem startowym lub ogromna góra nie warto na poczatek budowac szybkiego "dolnoplata" lub szybowca o rozpiêtosci skrzydel 3 m bo szkoda pieniedzy. Wiêkszosc modelarzy rozbija i naprawia swoje pierwsze modele lub w najgorszym przypadku po prostu je kasuje wraz z osprzetem.
3. Nie wywazaj otwartych drzwi - wiele ciekawych i prostych rozwiazañ technicznych odszukasz na prywatnych stronach internetowych, lub witrynach wytwórców….
4. Lepiej zapytaj doswiadczonego modelarza przed startem bo po pierwszym samodzielnym starcie moze byc juz za pózno ….
5. mozna duzo pieniedzy zaoszczedzic kupujac poniektóre rzeczy uzywane,
przynajmniej dla tych mniej zamoznych, na stronach internetowych po konsultacjach z bardziej doswiadczonym modelarzem…
- Wlosnica — pila wlosowa, laubzega, metalowa ramka przystosowana do zakladania, cienkich (wloskowatych) pilek do drzewa i do metalu — uniwersalne narzedzie modelarza do wycinania zeber, wreg i innych czesci modeli ze sklejki, deseczek, tworzyw sztucznych i metalu.
Brzeszczot pilki do metalu — uniwersalna pilka do ciecia grubszych listewek, wykonywania naciec w zeberkach i podluznicach. Jako pilka do drzewa brzeszczot taki ma wiele zalet — nie szarpie materialu i umozliwia wykonanie waskich naciêc. Poza tym moze byc uzywany zgodnie z przeznaczeniem — do ciecia drobnych czesci metalowych. Modelarze uzywaja takich pilek zazwyczaj bez oprawek, które sa zbyt ciezkie. Z jednej strony mozna brzeszczot okleic. papierem i zrobic cos w rodzaju raczki.Szczypce uniwersalne, plaskie — do giecia czêsci metalowych, ciecia drutu i prac montazowych
- Pilnik pólokragly, tzw. zdzierak (Nr O lub Nr l), o dlugoœci 250 mm — do pilowania czesci drewnianych plaskich (plaska strona pilnika) i wkleslych (strona pólokragla).
- Rozwiertak uniwersalny — do wykonywania niewielkich otworów. W handlu niedostepny, mozna wykonac samemu przez opilowanie kawalka drutu stalowego (np. z grubej szprychy) nadajac mu zwezajacy sie, ostry ksztalt o przekroju, czworokatnym lub trójkatnym. Doskonale rozwiertaki wykonuje sie ze starych pilników przez oszlifowanie.
- Pilnik okragly, tzw. równiak (Nr l), o dlugosci 160 lub 200 mm — do poprawiania i powiekszania wykonanych rozwiertakiem otworów.
- Malotek, maly, 100-gramowy — potrzebny przy wykonywaniu drobnych czesci metalowych oraz do przybijania konstrukcji do deski montazowej.
- Wkretak (srubokret), o szerokosci 6 mm — do przykrecania wkretów
- Imadlo równolegle, przenosne, przykrecane do stolu, o szerokosci szczek 60—80 mm — potrzebne przy obróbce bardziej precyzyjnych detali.
- Wiertarka reczna, jedno-przekladniowa — do wiercenia otworów w blokach zeberek i w innych czesciach modeli.
- Wiertla krete, o róznych srednicach — od 1,0 do 6,0 mm.
- Punktak, tzw. znacznik — do zaznaczania miejsca otworu przed nawierceniem.
- Strug z nastawnym ostrzem, najlepiej maly metalowy, o dlugosci 100 lub 150 m — do strugania listewe.
- Dlutko pólokragle, tzw. zlobak, o szerokoœci 8 mm — do drazenia kadlubów oraz owiewek z drzewa.
- Tarnik, zdzierak i gladzik, o dlugosci 200—250 mm — do zgrubnej obróbki duzych czesci drewnianych oraz smigiel.
- Pilniki slusarskie, plaski, pólokragly i okragly, zdzieraki (Nr 1) i gladziki (Nr 2) — do wykañczajacej obróbki czesci drewnianych i metalowych. Najkorzystniejsze dlugosci 160 lub 200 mm.
- Pilniki igielkowe (iglakli, plaski, okragly, kwadratowy i nozowy, o dlugosci ostrza 80 mm — do wykañczajacej obróbki ksztaltowych otworów, glównie w metalu (blachach).
- Szczypce okragle — do giecia drutu.
- Szczypce — do ciecia drutu, dlugosc 100 mm.
- Lutownica (kolba), elektryczna 220 V/100 W lub 110 V/60 W, najlepsza plaska z zalanym hermetycznie wkladem grzejnym lub transformatorowa, pasta do lutowania, cyna — niezbedne przy wykonywaniu zbiorników, podwozi i innych mechanizmów
Pinceta, dlugosci 100 i 160 mm — do montowania precyzyjnych czesci modeli.
Dlutka plaskie, o szerokosci 2 i 4 mm.
- Dlutka pólokragle, o szerokosci 2 i 4 mm.
- Imadelko reczne — pomocne przy wykonywaniu drobnych czesci modelu.
- Gwintowniki: M2, M3, M4, M5 i M6 wraz z pokretlem — do wykonywania gwintowanych otworów w metalowych, i plastykowych czesciach modeli.
- Narzynki do gwintów zewnetrznych: M2, M3, M4, M5 i M6 z oprawka— do gwintowania drutów i wykonywania nietypowych srub.
- Suwmiarka — do pomiarów warsztatowych.
- Komplet kluczy plaskich, oczkowych, nasadowych, swiecowych 3,5; 4,5; 5,5; 6; 7; 8; 10; 13.
Miniwiertarka elektryczna z mozliwoscia zalozenia gietkiego walka z uchwytem do ksztaltowych frezów i kamieni szlifierskich — do przeróbek (forsowanie) wyczynowych silników.
- Komplet frezów, tarcz i kamieni szlifierskich (dentystycznych).
- Mikrowyzynarka elektryczna.
- Mikroszlifierka oscylacyjna.
- sruba mikrometryczna — do pomiarów precyzyjnych czesci.
- Tokarka z kompletem nozy.
- Gwintownik calowy 1/4", 32 zwoje na cal.
Multimetr - do mierzenia podstawowych wartosci elektrycznych.
Troche teori
|
Podstawy aerodynamiki |
|
AERODYNAMIKA I MECHANIKA LOTU
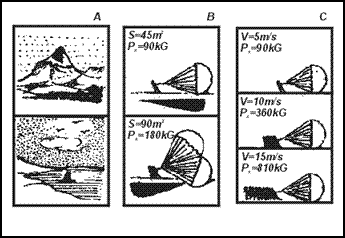
Rys. 1. Opór ciała w ruchu: A — kula, B — kształt opływowy, C — wartość współczynników oporu różnych ciał o tej samej powierzchni przekroju poprzecznego.
Rys. 2. Powierzchnie: A — czołowa przekroju poprzecznego ciała (1). B — przekroju poprzecznego skrzydła (2 — profil), C — powierzchnia nośna
1. kształtu ciała, gładkości jego powierzchni i ustawienia go względem kierunku ruchu; 2. gęstości powietrza, 3. wielkości powierzchni ciała, 4. kwadratu prędkości ruchu.
Rys. 3. Od czego zależy opór: A—od gęstości powietrza (w górach rzadkie, nad morzem gęste), B —od powierzchni, C — od prędkości. |
|
Strona 2 z 7
Rys. 4. Latawiec i powietrze: A — chłopiec biegnie w ciszy, B — wiatr wleje, C — tunel aerodynamiczny.
Rys. 5. Zależność współczynnika oporu cx od kąta natarcia (alfa)
|
Strona 3 z 7
A jak powstaje siła nośna? Aby wytłumaczyć to zjawisko, należy dokonać paru obserwacji. Gdzie rzeka płynie szybciej: tam gdzie jest szeroko rozlana, czy tam gdzie jest wąska? Łatwo można zauważyć, te im koryto rzekł jest węższe, tym prąd bardziej rwący. Jest to tak zwiana zasada ciągłości, którą zapamiętamy w następującej formie: „gdy przekrój maleje, to prędkość wzrasta”.
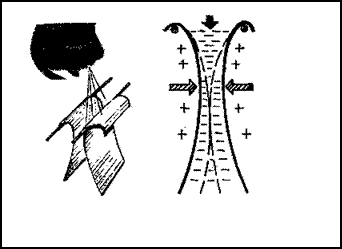
Zróbmy teraz następujące doświadczenie. Weźmy dwie pocztówki, które po wygięciu jak na rys. 6 zawiesimy na dwóch drutach. Co się stanie, gdy dmuchniemy między nie? Czy oddalą się od siebie? Ku naszemu zdumieniu — zbliżą się. Dlaczego?
Zastanówmy się nad tym, co działo się z powietrzem podczas doświadczenia? Dmuchamy między pocztówki. Gdy powietrze wpada w zwężenie między pocztówkami, to zgodnie z zasadą ciągłości prędkość jego wzrośnie. Lecz w przyrodzie nic nie dzieje się za darmo. Prędkość powietrza, czyli jego energia ruchu (energia kinetyczna), mogła śle zwiększyć tylko czyimś kosztem, w tym wypadku kosztem ciśnienia powietrza (czyli energii potencjalnej), tzn. ciśnienie powietrza musiało zmaleć. To właśnie pokazuje nam doświadczenie z pocztówkami. Ciśnienie miedzy pocztówkami zmalało, więc ciśnienie powietrza otaczającego z zewnątrz pocztówki docisnęło je do siebie.
Doświadczeniem naszym odkryliśmy zasadnicze prawo aerodynamiki, które nosi nazwę prawa Bernoulliego. Zapamiętajmy, że „gdy prędkość wzrasta, to ciśnienie maleje i odwrotnie, gdy prędkość maleje — ciśnienie wzrasta".
Przy okazji powinniśmy się zapoznać z kilkoma określeniami. Ciśnienie powietrza nazywamy ciśnieniem statycznym. Energie ruchu powietrza, tak dobrze odczuwane na twarzy podczas jazdy motocyklem, nazywamy ciśnieniem dynamicznym.
Czasami możemy się spotkać z innym sformułowaniem prawa Bernoulliego: „Suma ciśnień statycznego i dynamicznego jest stała". Jest, to dosłownie to samo co poznaliśmy tylko powiedziane za pomocą terminów fachowych.
Znając zasadę ciągłości i prawo Bernoulliego możemy wyjaśnić jak powstaje siła nośna na skrzydle. Jeśli przyjrzeć się rysunkowi, to widać, że powietrze przepływające nad skrzydłem wpada jakby w zwężenie na rzece, więc jego prędkość musi wzrosnąć. Jak już wiemy z prawa Bernoulliego, wzrost prędkości powoduje spadek ciśnienia. Nad skrzydłem ciśnienie zmaleje, pod skrzydłem będzie ciśnienie większe. Różnica tych ciśnień wywołuje siłę, która nazywamy siłą nośną. A jak będzie z siłą nośną na profilu symetrycznym (Rys. 7)? Przy zerowym kacie natarcia nie będzie jej. Lecz przy ustawieniu skrzydła pod kątem większym od zera już się pojawi, gdyż opływ powietrza nad i pod profilem nie będzie symetryczny.
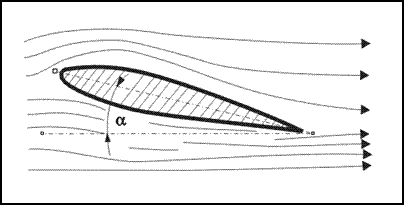
Rys. 7. Profil symetryczny przy dodatnim kącie natarcia (alfa)
Opisane zjawisko nie zawsze jednak występuje. Siła nośna powstaje na profilu tylko przy kątach natarcia do około 19o. Gdy kąt natarcia jest większy, strugi powietrza odrywają się od skrzydła i siła nośna gwałtownie maleje (skrzydło traci nośność). Zawirowania zmieniają wtedy opływ profilu i podciśnienie nad skrzydłem gwałtownie maleje. Równocześnie silnie wzrasta opór.
Siła nośna tym się różni od innych sił podtrzymujących ciała, np. od siły unoszącej łódź na wodzie, że skrzydło może stracić siłę nośną przez nadmierne zwiększenie kąta natarcia. Przekroczenie kąta oderwania strug wywołuje nagła utratę siły nośnej i prędkości, przepadnięcie oraz może spowodować korkociąg.
Siła nośna tak jak opór zależy od:
1. kształtu ciała i jego kąta natarcia względem kierunku ruchu,
2. gęstości powietrza,
3. wielkości powierzchni nośnej,
4. kwadratu prędkości ruchu.
Powyższą zależność możemy zapisać w postaci wzoru:
w którym:
Pz, — silą nośna,
cz, — współczynnik siły nośnej,
pozostałe oznaczenia jak we wzorze na opór (powstawanie siły nośnej przedstawia rys. 9).
Rys. 9. Powstawanie siły nośnej (Pz) „—" małe ciśnienie (podciśnienie), „+" duże ciśnienie (nadciśnienie)
Współczynnik Cz (rys. 10) mierzy się w tunelu aerodynamicznym (podobnie jak cx). Wygląd wykresu cz w zależności od a jest związany z kształtem profilu i dla każdego profilu jest trochę inny. Ciała, które dają dużą siłę nośną, różnią się kształtem od ciał o najmniejszym oporze. 'Warunkiem dużej siły nośnej jest krzywizna profilu. Płaska płytka daje parokrotnie mniejszą siłę nośną niż wygięta.
Rys. 10. Zależność współczynnika siły nośnej (cz) od kąta natarcia (alfa)
Profile lotnicze dzielimy na: wklęsłe, płaskie, dwuwypukłe i symetryczne (rys. 11). Wklęsłe stosowane są do powolnych szybowców. Płaskie obecnie są prawie nie używane. Najczęściej stosowane są dziś dwuwypukłe. Symetryczne przede wszystkim jako profile usterzeń.
Rys. 11. Rodzaje profili lotniczych: A — wklęsły, B — płaski, C — dwuwypukły, D — symetryczny
Mówiąc o profilach powinniśmy się zaznajomić z takimi pojęciami jak cięciwa oraz dodatni i ujemny kąt natarcia (rys. 12). Cięciwą geometryczną nazywamy linię łączącą krawędź natarcia z krawędzią spływu. W przypadku profilu płaskiego lub wklęsłego cięciwą jest linia styczną do spodniej strony profilu. Jest to linia, od której mierzymy kąt natarcia. Kierunek wyznaczony przez kąt natarcia, przy którym siła nośna profilu równa się zeru, nazywamy linią zerowej siły nośnej lub cięciwą aerodynamiczną.
Kąt natarcia nazywamy dodatnim jeżeli powietrze napływa na skrzydło od jego spodu, ujemnym — jeśli od strony górnej.
Rys. 12. Profil (A): n — krawędź natarcia, c — cięciwa, s — krawędź spływu. Kąt natarcia (alfa): A — zerowy. B — dodatni, C — ujemny.
Grubość profilu określamy tzw. grubością procentową. Jest to stosunek maksymalnej grubości profilu do długości cięciwy podany w procentach. Profile cienkie mają grubość 6—9%, średnie około 12%, grube powyżej 15%.
Strona 4 z 7
B. Biegunowa samolotu i biegunowa prędkości.
Dalsze rozważania uprośćmy do szybowca, jako samolotu poruszającego się bez napędu. Według pierwszej zasady Newtona, którą zapewne znacie z fizyki, ciało porusza się ruchem jednostajnym prostoliniowym (lub znajduje się w spoczynku), jeśli działające nań siły się równoważą. Zastosujemy tę zasadę do lotu szybowca. Jakie siły działają na szybowiec? Ciężar, siła nośna l opór. Jeśli dwie siły działają na jakieś ciało, np. dwóch chłopców ciągnie linę w przeciwne strony sprawa jest prosta. Siły się równoważą, gdy każdyz chłopców ciągnie tak samo mocno. Co zaś zrobić, gdy mamy trzy siły i każda działa w inną stronę? Trzeba znaleźć wypadkową dwu z nich i dopiero ta wypadkowa ma być równa trzeciej sile. W przypadku samolotu silnikowego dochodzi czwarta siła związana z ciągiem układu silnik/śmigło. Wypadkową dwóch sił znajdujemy, rysując tzw. równoległobok sił (rys. 13).
Wprowadzimy najpierw pojęcie doskonałości szybowca. Doskonałością nazywamy stosunek odległości (L) jaką przeleci szybowiec, do wysokości (H), którą straci na ten lot — lub prościej odległość w metrach którą przeleci szybowiec z wysokości 1 m.
Z
Rys. 13. Rozkład sił aerodynamicznych w locie P — wypadkowa siła aerodynamiczna, Q — masa szybowca
Rys. 16. Od czego zależy opór indukowany A — widok. z przodu. B — widok z góry; 1 — ucieka dużo powietrza. 2 — ucieka mało powietrza
Rys. 17. Wydłużenie płata (A) i obrys skrzydeł (B); 1 — eliptyczny, 2 — prostokątno-trapezowy, 3 — trapezowy, 4 — prostokątny.
Rys. 18 Ruch burzliwy (A) i laminarny (B); P - punkt przejścia; 1 — profil zwykły, 2 — profil laminarny
Strona 5 z 7
W którym v – prędkość modelu [m/s], d – cięciwa skrzydła [mm]
Za pomocą tej liczby można porównywać ze sobą różne modele i upewnić się czy ich lot nie będzie się czasem odbywał w warunkach krytycznych. Rozróżniamy trzy zakresy związane z liczbą Reynoldsa:
a) zakres pierwszy – tak zwany nadkrytyczny lub turbulentny Re > 60 000 ma miejsce przy większych prędkościach i przy większych rozmiarach modelu; strumień powietrza opływający płat ma wówczas dużą energię, w warstwie przyściennej jest silnie zaburzony i dobrze przylega do krzywizny profilu, wskutek czego zawirowania poza skrzydłem są niewielkie a skrzydło posiada mały opór i dużą siłę nośną,
b) zakres drugi – tak zwany krytyczny lub przejściowy 25 000 < Re < 60 000 odbywa się wówczas gdy zmniejszymy rozmiary skrzydła, lub prędkość modelu; strugi powietrza tracą swoją energię, miejscami jakby odklejają się od górnej powierzchni skrzydła, powstają niekorzystne zawirowania, wzrasta opór i maleje siła nośna, a lot modelu jest chwiejny i niepewny,
c) zakres trzeci – tak zwany podkrytyczny lub laminarny Re < 25 000 dalsze zmniejszenie wymiarów skrzydła lub też jego prędkości powoduje ustalenie się wokół skrzydła spokojnego, warstwowego opływu; energia opływającego profil powietrza jest bardzo mała; lot w zakresie podkrytycznym jest spokojny.
Przy ruchu burzliwym występuje opór parokrotnie większy niż przy laminarnym, gdyż skrzydło jest hamowane przez znacznie większe, ilości cząsteczek. To czy ruch cząsteczek po skrzydle będzie laminarny czy burzliwy, zależy od kształtu, profilu oraz jego gładkości. Jeśli skrzydło będzie miało profil laminarny oraz będzie wypolerowane i jego szorstkość nie będzie przekraczać 1/100 mm — to na dużej części profilu opływ będzie laminarny i skrzydło będzie stawiać mały opór. Jednakże takie skrzydło jest trudne do wykonania. Drobne zanieczyszczenia psują jego zalety. Dlatego też profile laminarne stosuje się tylko na szybowcach wyczynowych. Na ogół szkolne szybowce mają profile zwykłe, na których powietrze tylko na małym odcinku ma ruch laminarny w warstwie przyściennej, na większej części profilu posuwa się ono ruchem burzliwym. Szybowce z profilami laminarnymi osiągają doskonałość 36—59.
Na biegunowej płatowca znajduje się parę punktów, które powinien znać każdy modelarz. Pierwszy punkt charakterystyczny to kąt maksymalnej siły nośnej, czyli oderwania strug. Przekroczenie tego kąta powoduje utratę siły nośnej. Drugi, położony trochę wyżej od pierwszego — to kąt najmniejszego opadania (zwany ekonomicznym). Jest to kąt natarcia, przy którym szybowiec ma najmniejszą prędkość opadania. Trzeci – kąt największej doskonałości umożliwia lot z najmniejszą utratą wysokości. Czwarty — to kąt natarcia przy pionowym nurkowaniu. Przy pionowym nurkowaniu siła nośna równa się zeru — stąd punkt ten leży na przecięciu biegunowej z osią. Poniżej tego punktu znajduje się zakres lotu odwróconego („plecowego"). Oczywiście dla każdego szybowca, biegunowa ma trochę inny wygląd trochę inne kąty natarcia odpowiadają punktom charakterystycznym.
Wróćmy jeszcze do rysunku 13. Jeśli przyjąć, że kąt lotu szybowca względem poziomu jest niewielki (to znaczy szybowiec leci prawie poziomo), wypadkowa siły nośnej i oporu nie będzie wiele większa od siły nośnej. Wtedy możemy powiedzieć, że w przybliżeniu siła nośna równa się ciężarowi oraz możemy napisać:
Z wzoru tego widzimy, że prędkość lotu wzrasta ze wzrostem, obciążenia powierzchni Q/S, czyli gdy maleje powierzchnia nośna lub wzrasta ciężar modelu oraz ze zmniejszeniem cz, czyli ze zmniejszeniem kąta natarcia. Ponadto prędkość lotu będzie rosła z nachyleniem toru lotu szybowca ku ziemi — co przed chwilą pozwoliliśmy sobie pominąć.
Prócz doskonałości i prędkości lotu interesuje nas jeszcze prędkość opadania i promień zakrętu. O zakręcie pomówimy później. Teraz zajmiemy się opadaniem. Znając biegunową szybowca, jego ciężar i wielkość powierzchni nośnej, można obliczyć nie tylko prędkość lotu, lecz również prędkość opadania.
Wyniki tych obliczeń zazwyczaj przedstawia się w postaci wykresu. Jest to najważniejsza krzywa w szybownictwie (zarówno modelarskim jak i prawdziwym), tzw. biegunowa prędkości (Rys. 21).
Rys. 21.Biegunowa prędkości: v — prędkość lotu, w — opadanie, wmin — opadanie najmniejsze, vek - prędkość najmniejszego opadania, vopt — prędkość największej doskonałości, alfa — kąt największej doskonałości
Rys. 22. Lot z wiatrem i pod wiatr: A — tor lotu bez wiatru, B — tor lotu pod wiatr, C — tor lotu z wiatrem
Rys. 24 — Szybowiec w „kominie" opada wzglądem powietrza, a wznosi się względem ziemi; 1 — schody ruchome, 2— winda, A — las, B — zboże, C — piasek, D — woda, E — prądy wznoszące
Strona 7 z 7
Rys. 25. Rodzaje równowagi
Rys. 26. Obroty szybowca wokół osi podłużnej (A — przechylanie), poprzecznej (B — pochylanie), pionowej (C — zmiana kierunku, odchylenie)
Rys. 27. Wędrówka środka parcia
Rys. 28. A — stateczność podłużna: 1 — równowaga momentów (Mp — moment od płata, Mu — moment od statecznika poziomego. Q — masa), 2 i 3 — duży moment od statecznika poziomego (powoduje obrót szybowca); B — kąt zaklinowania statecznika poziomego względem cięciwy skrzydła (alfa)
Rys. 29. Działanie statecznika pionowego: A - kierunek lotu, B - siła na stateczniku pionowym, C - kierunek obrotu szybowca
Prócz stateczności wymagamy od modelu, by nie wpadał samoistnie w korkociąg. Przyczyną korkociągu jest przeciągnięcie modelu i oderwanie się strug na jednym ze skrzydeł. Wtedy na tym skrzydle opór wzrasta, na drugim zaś jest mały. Jedno skrzydło zostaje w tyle, drugie zaś idzie do przodu. Model zaczyna kręcić korkociąg. Aby zabezpieczyć się przed korkociągiem, należy się postarać, by w razie przeciągnięcia oderwanie strug wpierw nastąpiło w pobliżu kadłuba, a najpóźniej na końcach skrzydeł w pobliżu lotek. Wtedy model będzie przepadał, lecz nie wejdzie w korkociąg, a lotki będą nadał skutecznie działać. Możemy to uzyskać odpowiednią budową skrzydła np. przez, takie skręcenie skrzydła, przy którym na jego końcu mamy mniejsze kąty natarcia niż przy kadłubie.
Rys. 31. Dziabnie skręcenia skrzydeł: A — mały kąt natarcia — na końcach skrzydeł strugi nie odrywają się, B — duży kąt natarcia przy kadłubie strugi odrywają się
Rys. 30. Wpływ wzniosu skrzydeł na stateczność boczną szybowca: 1—oś podłużna szybowca, 2 —kierunek lotu z przechyleniem i ześlizgiem w bok na skrzydło (3). 4 — duża siła nośna, 5 — mała siła nośna. A. — wznios skrzydeł w widoku z przodu oraz kąt wzniosu skrzydła.
Usterzenie pionowe działa jak chorągiewka na dachu. Ciągnie szybowiec za ogon, by powrócił do dawnej pozycji, to znaczy, leciał wzdłuż kierunku ruchu. Gdyby nie było usterzenia pionowego — szybowiec przy każdym bocznym podmuchu wiatru tańczyłby, zamiatając ogonem na wszystkie strony i zmieniałby wciąż kierunek lotu.
A jak przedstawia się stateczność poprzeczna? Szybowiec jej nie posiada i przy przechyleniu na skrzydło sam nie powraca do pozycji poziomej, zwykle pilot musi wychyleniem lotek przywrócić szybowcowi właściwe położenie. Ktoś mógłby powiedzieć, że przecież latają modele, które nie mają pilota sterującego totkami, jednak nie przewracała się przez skrzydło? Coś w tym musi być. Otóż szybowiec posiada stateczność boczną. Co to takiego? Jeśli szybowiec przechyli się i zacznie się ślizgać w bok na skrzydło strugi powietrza będą opływać szybowiec z boku. Jeśli napotkają one tylko usterzenie pianowe to przytrzymają go za ogon i zmuszą do spirali. Jeżeli zaś skrzydło będzie końcami wzniesione ku górze, to powietrze będzie również działać na skrzydło. Spowoduje wtedy wzrost siły nośnej na tym skrzydle, w kierunku którego szybowiec się ślizga. Siła ta uniesie skrzydło do góry i szybowiec wróci do normalnej pozycji. Tak więc wznios skrzydeł może zapewnić stateczność boczną.
Czy może istnieć stateczny szybowiec bez usterzenia? Tak, o ile skrzydło ma tzw. profil samostateczny. Profil samostateczny ma podgiętą do góry krawędź spływu, co powoduje że wędrówka środka parcia jest u niego przeciwna niż w zwykłym profilu. Pozornie, bez usterzenia są bezogonowce o skrzydłach ze skosem do tyłu. Faktycznie rolę usterzenia spełniają końce skrzydeł, które znajdują się w tyle za środkiem ciężkości modelu i mają mniejszy kąt natarcia niż środkowa część skrzydła.
Mówiąc o stateczności liczyliśmy momenty względem środka ciężkości szybowca. Lecz czy środek ciężkości zawsze jest punktem stałym? Otóż nie. Jak wiadomo, środek ciężkości jest to punkt „przyczepienia” wypadkowej ciężaru wszystkich części szybowca. Ciało podparte w środku ciężkości zachowuje równowagę obojętną. Weźmy drążek. Aby utrzymać go na palcu poziomo — trzeba go podeprzeć w środku ciężkości, który znajduje się w połowie długości drążka. Jeśli na końcu drążka zawiesimy ciężarek — środek ciężkości przesuwa się w stronę ciężarka. Jeśli ciężarek zwiększymy lub przesuniemy — przesunie się również i środek ciężkości. Tak samo położenie środka ciężkości modelu zależy od zmiany położenia jakiegoś ciężaru oraz od zmiany jego wielkości, na przykład od tego, czy zbiorniczek paliwa jest pełny czy pusty.
Położenie środka ciężkości nazywamy wyważeniem. Przesuniecie środka ciężkości do przodu (czyli wyważenie przednie) polepsza stateczność, przesunięcie do tyłu spowoduje, że model będzie zadzierał aż do oderwania się strug. Dlatego tylne wyważanie jest niedopuszczalne. Możemy to łatwo sprawdzić. Weźmy dobrze latający model kartonowy i przesuwajmy mu obciążenie do tyłu. Dość szybko doprowadzimy do przeciągnięcia modelu, a tym .samym lotu niestatecznego.
Na statecznośc kierunkową szybowca najsilniej wpływa statecznik pionowy.
Aby tego uniknąć, stosujemy statecznik poziomy. Jakie Jest działanie tego statecznika? Jeżeli szybowiec ma być stateczny, to momenty względem środka ciężkości — od siły nośnej skrzydła i od usterzenia — muszą przywracać mu zawsze położenie, z którego został wytrącony. Jak się zachowa więc nasz szybowiec z usterzeniem? Póki szybowiec leci prostym lotem ślizgowym — momenty się równoważą. Gdy np. z powodu podmuchu wzrośnie kąt natarcia na skrzydle, środek parcia przesunie się do przodu i wzrośnie siła nośna. Na usterzeniu również wzrośnie siła nośna. Zauważmy jednak, że odległość usterzenia od środka ciężkości jest wielokrotnie większa niż odległość środka parcia skrzydła od środka ciężkości. Przeto wzrost momentu od usterzenia będzie większy niż momentu skrzydła i ogon zostanie podniesiony do góry, przez co szybowiec wróci do normalnego położenia. Podobna sytuacja powstanie przy ujemnych kątach natarcia. Widzimy wiec, że statecznik zapewnia szybowcowi stateczność podłużną.
Ponadto od statecznika (i steru) zależy równowaga szybowca w locie. Jeśli na końcu kija podpartego w środku uwiesić ciężar, to ażeby uzyskać równowagę, na drugim końcu też trzeba zawiesić ciężar. Podobnie gdy na kadłub przed środkiem ciężkości działa siła nośna skrzydła, to na tyle kadłuba do równowagi potrzebna jest siła od usterzenia. Zależy ona od kąta zaklinowania statecznika względem cięciwy skrzydła, który winien być ujemny.
Przy okazji przypatrzmy się rysunkowi 26 i zapamiętajmy, jakie obroty modelu nazywamy: pochyleniem, przechyleniem i zmianą kierunku (odchyleniem). Stateczność podłużna modelu zależy od momentów sił powodujących pochylenie się szybowca. A co to jest moment? Momentem nazywamy działanie siły powodującej obrót ciała. Wielkość momentu zależy nie tylko od wielkości siły, lecz również od długości ramienia, na które siła działa.
Zainteresujmy się momentem siły nośnej skrzydła. Podciśnienie nad profilem i nadciśnienie pod spodem profilu zmieniają się w zależności od kąta natarcia. Przy dużych kątach dodatnich większe jest nad- i podciśnienie bliżej krawędzi natarcia. Przy ujemnych — bliżej krawędzi spływu. Siła nośna powstała jako wypadkowa tych ciśnień, będzie więc raz „przyczepiona” bliżej przodu, a raz bliżej tyłu. Ten punkt przyczepienia siły nazywamy środkiem parcia, opisane zaś zjawisko — wędrówką środka parcia.
Jeżeli środek ciężkości, dookoła którego — jak wiemy — model się obraca, znajduje się w miejscu oznaczonym kółkiem na rys. 27 to zauważymy, że szybowiec posiadający tylko skrzydło będzie niestateczny. Na dużych kątach natarcia siła nośna — przyczepiona przed środkiem ciężkości — będzie zadzierała przód szybowca w górę i to coraz silniej. Na małych kątach natarcia siła nośna zmusi szybowiec do coraz ostrzejszego nurkowania. 'Widzimy wiec, ze szybowiec mający jedynie skrzydło będzie chciał stawać dęba albo nurkować — aż do przejścia na plecy.
Ciało znajdujące się w równowadze trwałej zawsze wraca do pierwotnego położenia i nazywamy je statecznym. Model nazywamy statecznym, jeśli bez pomocy pilota utrzymuje stałą prędkość lotu (stały kąt toru lotu), stały kierunek lotu i nie wchodzi w spiralę. Ponieważ modelem może wykonywać ruchy wokół trzech osi obrotu — rozróżniamy trzy rodzaje stateczności: podłużną, kierunkową i poprzeczną.
Jakie są skutki tego, gdy szybowiec wleci w prądy wznoszące czy opadające — chyba wiecie lub się domyśliliście. Warto jednak zwrócić uwagę na to, że szybowiec zawsze opada względem powietrza, które go otacza; podobnie jak saneczki po zboczu góry szybowiec potrafi tylko ześlizgnąć się na dół. Wznosi się zaś w górę tylko dzięki temu, że powietrze, w którym szybowiec opada, szybciej winduje się w górę, niż opada w dół. Można więc szybowiec porównać do piórka, które puściliśmy pod sufitem windy. Piórko opada ku podłodze, lecz równocześnie winda wznosi się szybko w górę. Innym porównaniem mogą być ruchome schody, jadące do góry, z chłopcem, który próbuje zejść po nich na dół.
Można z niej odczytać prędkość opadania dla każdej prędkości lotu oraz doskonałość i kąt toru lotu. Np. na naszym rysunku dla prędkości v = 75 km/h (punkt A na krzywej) opadanie wyniesie 2,7 m/s, zaś doskonałość d=14. Z biegunowej prędkości odczytujemy najmniejsze opadanie kreśląc linię poziomą styczną do biegunowej, a doskonałość — prowadząc styczną do krzywej z początku układu osi 0.
Re = 70*v*d
Najmniejszy opór wzbudza skrzydło eliptyczne, potem prostokątno-trapezowe i trapezowe. Największy—prostokątne z niezaokrąglonymi końcami.
Poznaliśmy już opór skrzydła. Aby otrzymać opór całego szybowca, musimy do oporu skrzydła dodać opór kadłuba, usterzenia i wszystkich części wystających oraz opory spowodowane zawirowaniami w miejscach łączenia poszczególnych części szybowca z sobą (tzw. opory interferencyjne).
Dopiero teraz, gdy znamy opór, a raczej współczynnik całkowitego oporu szybowca — dla rożnych kątów natarcia — możemy przystąpić do wykreślenia biegunowej szybowca. Na osi poziomej odmierzamy cx całego szybowca dla danego kąta natarcia, na osi pionowej zaś cz, odpowiadający temu kątowi natarcia. Te dwie wartości wyznaczają nam punkt. Dla innego kąta natarcia otrzymamy inny punkt. Łącząc te wszystkie punkty otrzymamy krzywą o kształcie litery C. Jest to właśnie biegunowa szybowca, zwana czasami biegunową Lilienthala.
Jak teraz odczytać z biegunowej największą doskonałość? Jeżeli z punktu przecięcia, się osi wykreślimy styczną do biegunowej, to punkt styczności z krzywą odpowiada największej doskonałości szybowca. Możemy odczytać kąt natarcia przy maksymalnej doskonałości (np. =10o) oraz cz i cx i stąd obliczyć doskonałość. (W naszym przykładzie cz=0,81, cx=0,03, zaś d = cz/cx = 27). Doskonałość szybowców treningowych wynosi 20—28, wyczynowych 28—58. Od czego zależy doskonałość? Przede wszystkim od tych czynników, które wpływają na opór. Opór zaś szybowca możemy zmniejszyć, starając się, by było jak najmniej części wystających i nierówności oraz by nie było części o kształtach nieopływowych.
Najsilniej na doskonałość wpływa wydłużenie skrzydła, lecz ze względu na wytrzymałość nie można zbytnio zwiększyć rozpiętości szybowca. Poważnie też wpływa opór tarcia. Wielkość oporu tarcia zależy od tego, czy cząsteczki powietrza, przepływające wzdłuż powierzchni ciała, czyli w tzw. Warstwie przyściennej, czynią to spokojnie tzw. ruchem laminarnym, czy też burzliwie, tj. turbulentnie. Ruch laminarny i burzliwy możemy łatwo zaobserwować, puszczając wodę z kranu. Zaobserwujemy, że przy niewielkim odkręceniu kurka struga wody będzie ciągła, bez zawirowań, podczas gdy przy odkręceniu silnym woda wypływać będzie burzliwie — ruchem niespokojnym. (Rys. 18)
Gdzie więcej powietrza ucieka z dołu do góry? Na, końcu skrzydła szerokiego czy wysmukłego?
Widzimy od razu, że skrzydła wąskie i długie są lepsze. W lotnictwie smukłość skrzydła ocenia się za pomoce tzw. wydłużenia. Wydłużenie jest to stosunek rozpiętości skrzydła do jego (średniej) szerokości. Oznaczamy je literą l (lambda). Szybowce mają duże wydłużenie 15-20.
Opór indukowany zależy również od obrysu skrzydła (kształtu skrzydła w widoku z góry) oraz kształtu zakończenia skrzydła (rys. 17).
Do wykonania biegunowej musimy znać współczynniki siły nośnej i współczynnik oporu całego szybowca — dla różnych kątów natarcia. Znamy dotychczas jedynie cx profilu, opór zaś skrzydła składa się z oporu profilowego oraz oporu indukowanego (tzn. wzbudzonego) (rys. 16). Co to jest opór indukowany? Wyobraźmy sobie dwa skrzydła o tym samym profilu i tej samej powierzchni, lecz jedno krótkie i szerokie, a drugie wąskie i długie. Jak wiemy, nad skrzydłem panuje podciśnienie pod skrzydłem zaś nadciśnienie. A co się dzieje na końcu skrzydła? Zabrakło tu przegródki, jaką było skrzydło miedzy powietrzem o dużym i małym ciśnieniu. Powietrze zaczyna uciekać z dołu na górną powierzchnię skrzydła. Ponieważ skrzydło porusza się do przodu (szybowiec leci), powietrze zostanie zepchnięte do tyłu i tak powstanie za końcem skrzydła wir indukowany, który powoduje wzrost oporu skrzydła.
C. Stateczność i sterowność
Co to znaczy, że szybowiec jest stateczny? Aby to wyjaśnić, przypomnijmy sobie wiadomości o równowadze. Jak łatwo można się przekonać, istnieją 3 możliwości równowagi ciała: równowaga trwała, równowaga obojętna i równowaga nietrwała.
Rys. 23. Wpływ wiatru bocznego; A—tor lotu szybowca, B—tor lotu w ciszy, C — wiatr boczny
Biegunowa prędkości mówi też o doskonałości i opadaniu szybowca w przypadku wiatru przeciwnego i zgodnego oraz w razie znalezienia się w prądach wznoszących i duszących. Jeśli szybowiec będzie leciał pod wiatr, to jego prędkość względem ziemi będzie równa prędkości lotu minus prędkość wiatru. Gdy zaś leci z wiatrem, to prędkość względem ziemi jest sumą prędkości lotu i prędkości wiatru. Stąd pierwszy wniosek, że należy lądować pod wiatr, bo lepiej jest zetknąć się z ziemią na małej prędkości niż przy dużej, oraz że lecąc pod wiatr wylądujemy na znacznie mniejszym lotnisku. Lecąc z wiatrem zalecimy w tym samym czasie z danej wysokości znacznie dalej niż lecąc pod wiatr. Lecz nie zawsze lecimy prosto pod wiatr czy z wiatrem. Jaki więc będzie wpływ wiatru bocznego czy skośnego? Będzie on prócz tego znosił z kierunku. Aby utrzymać szybowiec na danym kursie, trzeba wtedy lecieć kierując model nie prosto na obrany cel, lecz nieco w bok, w stronę, skąd wieje wiatr.
Strona 6 z 7
stąd
Charakter przepływu definiuje tzw. Liczba Reynoldsa. Wiąże ona ze sobą prędkość poruszającego się ciała, jego wielkość jak też cechy (gęstość i lepkość) ośrodka w którym się porusza ciało. Upraszczając wzór do ruchu w powietrzu standardowym otrzymujemy wyrażenie na liczbę Reynoldsa:
Rys. 15. Biegunowa szybowca: A — przepadanie, B — kat przeciągnięcia, C — kąt najmniejszego opadania, D — kąt największej doskonałości, E — nurkowanie pionowe. F — lot plecowy.
Verantwortlich für den Inhalt dieser Seite ist ausschließlich der
Autor dieser Homepage, kontaktierbar über dieses Formular!